A gráfelmélet a matematika egyik legizgalmasabb és talán a legegyszerűbben megérthető területe. Gyakorlati alkalmazása azonban nagy bonyolultságú rendszerek megértését képes segíteni. A cikk célja hogy a területtel most ismerkedők egy kis inspirációt kapjanak.
A gráfelmélet története napjainkig
A gráfelmélet a svájci Euler nevéhez kapcsolódik, és egészen 1736-ig nyúlik vissza a története. A kezdeti gráfelméleti kutatások nem voltak kifejezetten komolynak mondhatók, akkor még nem igazán volt gyakorlati haszna az alkalmazásának. Mindenesetre remek rejtvények készültek az elmélet segítségével.
Az idő múlásával azonban egyre több felhasználási módja keletkezett a matematikai elméletnek. A 19. százdban már elektromos hálózatok, illetve molekuláris hálózatok körében is alkalmaztak gráfokat.
Napjainkban a gráfelmélet már sokkal átfogóbb tudományterület. Segítségével olyan összetett problémákat oldanak meg, mint a csővezeték-rendszerek áramlási problémái, vagy a logisztikai kihívások, útvonaltervezés. Tipikus, internetes alkalmazása a weboldalak linkhálózatának feltérképezése is, amit többek között a Google keresőmotorja is felhasznál (azonban ennek pontos módját sajnos nem ismerjük).
Mi a gráf?
Nemes egyszerűséggel a gráfok olyan pontokból és azokat összekötő vonalakból álló alakzatok, melyek valamilyen információt hordoznak (ez nem a matematikai megfogalmazás, inkább csak a saját értelmezésem).
Mire jó a gráfelmélet?
A legegyszerűbb példa, melyet Oystein Ore- A gráfok és alkalmazásaik című könyvében találunk a következő:
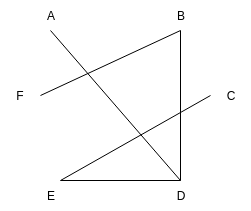
Az iskolai futballcsapat más iskolák csapataival együtt bajnokságon vesz részt. Összesen hat csapat indul, mindegyiküket egy betűvel jelöljük, így lesznek A, B, C, D, E és F csapatok. A verseny első néhány hetében már néhányan játszottak egymással de még közel sem mindenki mindenkivel. A meccseket itt gráfokkal jelölhetjük.
Gráf feladatok megoldással
a) Értelmezd a Gráfot
A fenti példában leírt állapotot tehát gráf segítségével követjük, ami így néz ki:
Feladat! Írd le hogy melyik csapat kivel játszott már!
Egy kis segítség – A D betűjelű csapat játszott a legtöbb ellenféllel!
b) Szögpontok és élek
A gráfok tehát pontokból és vonalakból állnak. Viszont ezek nem túl elegáns megnevezések. A pontokat szögpontnak, a vonalakat pedig éleknek nevezzük.
Feladat! Határozd meg hány éle és szögpontja van a fenti gráfnak
c) Rajzolj te is gráfot
A gráfelmélet legalapvetőbb részével eddigre készen vagy, most használd ki ezt a tudást. A feladat az előbbi focis példa alapján:
A versenyidény az utolsó részéhez érkezett. Rajzold meg a gráfot a csapatokról a következő információk alapján:
- Az E csapat kivételével minden csapat játszott már legalább 3 másikkal.
- A D csapat már játszott mindenkivel
- Az A csapat nem játszott a F-el és az E-vel
- Az F csapat pontosan 4 csapattal játszott
Források a gráfelméleti tudásom mélyítéséhez
- Gráfelmélet a Wikipédián
- Könyv – Oystein Ore: A gráfok és alkalmazásaik
Javasolj te is forrásanyagot hozzászólásként!